2009년 넷플릭스가 주최한 추천할고리즘 대회 후 우승자가 발표한 논문으로
해당 논문에서 ALS에 대한 설명이 있어 번역해보았다. (SVD를 찾다가 ALS 논문을 봐버렸다.. 사실 둘이 대칭점이 있어서 언제 써야 하는지는 알아둬야 할거 같다)
원문은 다음을 참조하세요.
https://datajobs.com/data-science-repo/Recommender-Systems-[Netflix].pdf
서문
넷플릭스 (Netflix Prize) 대회가 입증했듯이, 행렬 분해(Matrix Factorization) 모델은 제품 추천을 생성하는 데 있어 전통적인 최근접 이웃(Nearest-neighbor) 기법보다 우수합니다. 이는 암묵적 피드백, 시간적 영향, 그리고 신뢰도 수준과 같은 추가적인 정보를 통합할 수 있게 해주기 때문입니다.
Matrix Factorization (행렬 분해): 사용자-아이템 행렬을 두 개의 더 작은 행렬(사용자 특성, 아이템 특성)로 나누어 빈 공간(평점)을 예측하는 기법
Nearest-neighbor (최근접 이웃): 나와 취향이 비슷한 사용자(User-based)나 비슷한 아이템(Item-based)을 찾아 추천하는 고전적인 방식
Implicit feedback (암묵적 피드백): 클릭 기록, 구매 이력, 시청 시간 등 사용자가 직접 점수를 매기지는 않았지만 선호도를 유추할 수 있는 간접적인 데이터
Temporal effects (시간적 영향): 시간이 흐름에 따라 변하는 사용자의 취향이나 아이템의 인기를 의미
RecommendeR system stRategies
추천 시스템은 두 가지 전략 중 하나를 기반으로 합니다. 콘텐츠 필터링(Content Filtering) 방식은 각 사용자나 제품의 본질적인 특성을 나타내는 프로필을 생성합니다. 예를 들어, 영화 프로필에는 장르, 출연 배우, 박스오피스 인기 순위 등의 속성이 포함될 수 있습니다. 사용자 프로필에는 인구통계학적 정보나 설문조사를 통해 얻은 답변이 포함될 수 있습니다. 시스템은 이러한 프로필을 바탕으로 사용자와 그에 어울리는 제품을 연결합니다. 물론, 콘텐츠 기반 전략은 수집하기 어렵거나 아예 제공되지 않을 수도 있는 외부 정보를 모아야 한다는 전제가 필요합니다.
콘텐츠 필터링의 대안은 명시적인 프로필을 생성할 필요 없이 오직 사용자의 과거 행동(예: 이전 거래 내역이나 제품 평점)에만 의존하는 방식입니다. 이 접근 방식은 최초의 추천 시스템인 'Tapestry'의 개발자들이 만든 용어인 협업 필터링(Collaborative Filtering)으로 알려져 있습니다. 협업 필터링은 사용자와 사용자 사이의 관계, 그리고 제품 간의 상호 의존성을 분석하여 새로운 사용자-아이템 연관성을 식별합니다.
협업 필터링의 큰 매력은 특정 도메인에 국한되지 않으면서도(domain free), 콘텐츠 필터링으로는 프로필화하기 어렵고 파악하기 힘든 데이터의 측면들을 다룰 수 있다는 점입니다. 일반적으로 콘텐츠 기반 기법보다 정확도가 높지만, 협업 필터링은 시스템에 새로 진입한 제품이나 사용자를 처리하지 못하는 이른바 콜드 스타트(Cold Start) 문제를 겪습니다. 이 측면에서는 콘텐츠 필터링이 더 우수합니다.
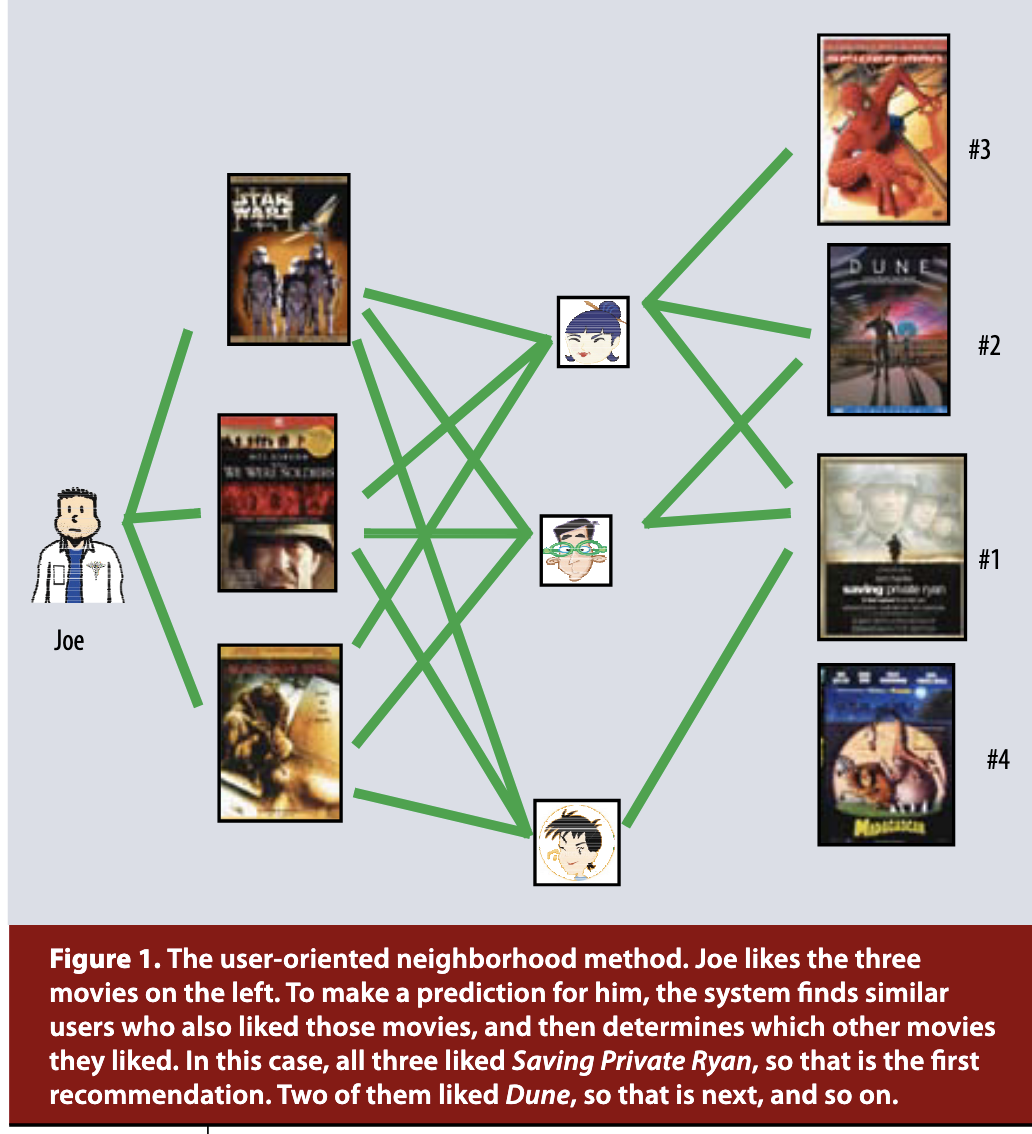
협업 필터링의 두 가지 주요 영역은 이웃 기반 메서드(Neighborhood methods)와 잠재 요인 모델(Latent factor models)입니다. 이웃 기반 메서드는 아이템 간의 관계 또는 사용자 간의 관계를 계산하는 데 중점을 둡니다. 아이템 기반(Item-oriented) 접근 방식은 동일한 사용자가 매긴 '이웃한' 아이템들의 평점을 바탕으로 해당 아이템에 대한 사용자의 선호도를 평가합니다. 어떤 제품의 이웃이란, 동일한 사용자에 의해 평가되었을 때 유사한 점수를 받는 경향이 있는 다른 제품들을 의미합니다. 예를 들어, 영화 <라이언 일병 구하기>의 이웃에는 다른 전쟁 영화, 스필버그 감독의 영화, 톰 행크스 출연 영화 등이 포함될 수 있습니다. 특정 사용자의 <라이언 일병 구하기> 평점을 예측하기 위해, 우리는 이 사용자가 실제로 평가한 영화들 중 해당 영화와 가장 가까운 이웃들을 찾습니다. 반면, 사용자 기반(User-oriented) 접근 방식은 서로의 평점을 보완해 줄 수 있는 취향이 비슷한 사용자를 식별합니다.
잠재 요인 모델(Latent factor models)은 평점 패턴에서 추론된 약 20개에서 100개 사이의 요인(factors)으로 아이템과 사용자의 특성을 규정하여 평점을 설명하려는 대안적 접근 방식입니다. 영화의 경우, 발견된 요인들은 코미디 대 드라마, 액션의 양, 아동 지향성 같은 명확한 차원을 측정할 수도 있고, 캐릭터 발달의 깊이나 기발함(quirkiness) 같이 덜 명확한 차원, 혹은 완전히 해석 불가능한 차원을 측정할 수도 있습니다. 사용자에게 있어 각 요인은 해당 영화 요인에서 높은 점수를 받은 영화를 그 사용자가 얼마나 좋아하는지를 측정합니다.
행렬 분해 방법 (Matrix Factorization Methods)
잠재 요인 모델을 가장 성공적으로 구현한 사례 중 일부는 행렬 분해에 기반하고 있습니다. 기본적인 형태의 행렬 분해는 아이템 평점 패턴에서 추론된 요인 벡터(vectors of factors)를 통해 아이템과 사용자 모두를 특징짓습니다. 아이템 요인과 사용자 요인 사이의 높은 일치성이 곧 추천으로 이어집니다. 이러한 방법들은 우수한 확장성(scalability)과 예측 정확도를 결합함으로써 최근 몇 년 동안 큰 인기를 얻었습니다. 또한, 다양한 실생활 상황을 모델링할 수 있는 뛰어난 유연성을 제공합니다.
추천 시스템은 다양한 유형의 입력 데이터에 의존하는데, 이 데이터는 대개 한 차원은 사용자를, 다른 차원은 관심 아이템을 나타내는 행렬에 배치됩니다. 가장 편리한 데이터는 고품질의 명시적 피드백(explicit feedback)으로, 이는 제품에 대한 사용자의 관심을 명시적으로 입력한 정보를 포함합니다. 예를 들어, 넷플릭스는 영화에 대한 별점 데이터를 수집하고, 사용자는 '좋아요'이나 '싫어요' 버튼을 눌러 TV 프로그램에 대한 선호도를 표시합니다. 이러한 명시적 사용자 피드백을 '평점(ratings)'이라고 부릅니다. 보통 명시적 피드백은 희소 행렬(sparse matrix) 형태를 띠는데, 이는 개별 사용자가 가능한 전체 아이템 중 아주 적은 비율의 아이템에만 평점을 매기기 때문입니다.
행렬 분해의 강점 중 하나는 추가적인 정보를 통합할 수 있다는 점입니다. 명시적 피드백을 사용할 수 없을 때, 추천 시스템은 암묵적 피드백(implicit feedback)을 사용하여 사용자 선호도를 추론할 수 있습니다. 이는 구매 이력, 검색 기록, 검색 패턴, 심지어 마우스 움직임과 같은 사용자 행동을 관찰함으로써 의견을 간접적으로 반영합니다. 암묵적 피드백은 보통 특정 사건의 발생 여부를 나타내므로, 일반적으로 데이터가 빽빽하게 채워진 밀집 행렬(dense matrix) 형태로 표현됩니다.
기본 행렬 분해 모델
행렬 분해 모델은 사용자-아이템 상호작용이 해당 공간에서의 내적(inner products)으로 모델링되도록, 사용자(user)와 아이템(item) 모두를 차원의 결합 잠재 요인 공간(joint latent factor space)에 매핑합니다. 이에 따라, 각 아이템 는 벡터 와 연관되고, 각 사용자 는 벡터 와 연관됩니다.
특정 아이템 에 대해, 의 요소들은 해당 아이템이 그 요인들을 양의 방향 혹은 음의 방향으로 얼마나 가지고 있는지를 측정합니다. 특정 사용자 에 대해, 의 요소들은 해당 요인이 높은 아이템에 대해 사용자가 얼마나 관심을 가지는지를 측정합니다.

결과적으로 나오는 내적 는 사용자 와 아이템 사이의 상호작용, 즉 아이템의 특성에 대한 사용자의 전반적인 관심을 포착합니다. 이는 사용자 의 아이템 에 대한 평점 rui의 값이 됩니다.
여기에서 중요한것은 각 아이템과 사용자를 요인 벡터 로 매핑하는 계산 과정입니다. 추천 시스템이 이 매핑을 완료하면, 식 (1)을 사용하여 사용자가 어떤 아이템에 부여할 평점을 쉽게 예측할 수 있습니다.
이러한 모델은 정보 검색 분야에서 잠재적 의미 요인을 식별하는 데 널리 사용되는 기법인 특잇값 분해(SVD, Singular Value Decomposition)와 밀접한 관련이 있습니다. 협업 필터링 도메인에 SVD를 적용하려면 사용자-아이템 평점 행렬을 분해해야 합니다. 하지만 사용자-아이템 평점 행렬의 희소성(sparseness)으로 인해 결측치(missing values)가 매우 많다는 점이 어려움을 유발합니다. 기존의 SVD는 행렬 정보가 불완전할 경우 정의되지 않습니다. 또한, 상대적으로 적은 알려진 데이터만 부주의하게 다룰 경우 과적합(overfitting)이 발생하기 쉽습니다.
초기 시스템들은 결측치를 채워 넣어 행렬을 밀집(dense)하게 만드는 대치법(imputation)에 의존했습니다. 그러나 대치법은 데이터 양을 대폭 증가시켜 계산 비용이 많이 들고, 부정확한 대치는 데이터를 심각하게 왜곡할 수 있습니다. 따라서 최근 연구들은 관측된 평점만을 직접 모델링하면서, 정규화(regularized) 모델을 통해 과적합을 피할 것을 제안합니다. 요인 벡터(와 )를 학습하기 위해, 시스템은 이미 알려진 평점 집합에 대해 정규화된 제곱 오차(squared error)를 최소화합니다.
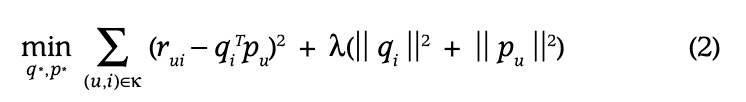
여기서 는 rui(사용자의 아이템에 대한 평점 근사치)가 알려진 쌍의 집합(훈련 세트)입니다.
시스템은 이전의 관측된 평점에 맞추어 모델을 학습합니다. 그러나 목표는 이러한 과거의 평점을 일반화하여 아직 알려지지 않은 미래의 평점을 예측하는 것입니다. 따라서 학습된 파라미터의 크기에 패널티를 주는 정규화를 통해 관측 데이터에 과적합되는 것을 방지해야 합니다. 상수 는 정규화의 정도를 조절하며, 보통 교차 검증(cross-validation)을 통해 결정됩니다.
학습 알고리즘 (Learning Algorithms)
식 (2)를 최소화하는 두 가지 접근 방식은 확률적 경사 하강법(Stochastic Gradient Descent, SGD)과 교대 최소 제곱법(Alternating Least Squares, ALS)입니다.
확률적 경사 하강법 (SGD) 사이먼 펑크(Simon Funk)는 식 (2)의 최적화를 위해 SGD를 대중화했습니다. 이 알고리즘은 훈련 세트의 모든 평점을 반복해서 훑습니다. 각 훈련 사례에 대해 시스템은 rui를 예측하고 그와 관련된 예측 오차를 다음과 같이 계산합니다

그 후, 시스템은 기울기(gradient)의 반대 방향으로 매개변수 의 크기만큼 수정합니다:

이 대중적인 접근 방식은 구현이 쉽고 실행 속도가 상대적으로 빠르다는 장점이 결합되어 있습니다. 하지만 어떤 경우에는 ALS 최적화를 사용하는 것이 유리할 때도 있습니다.
교대 최소 제곱법 (ALS) 와 가 모두 미지수이기 때문에 식 (2)는 볼록(convex) 함수가 아닙니다. 그러나 두 미지수 중 하나를 고정하면 최적화 문제는 이차식(quadratic) 형태가 되어 최적으로 해결될 수 있습니다. 따라서 ALS 기법은 들을 고정하는 것과 들을 고정하는 것을 번갈아 가며 수행합니다. 모든 가 고정되면 시스템은 최소 제곱 문제를 풀어 들을 다시 계산하고, 그 반대의 경우도 마찬가지입니다. 이는 수렴할 때까지 매 단계에서 식 (2)의 오차를 확실히 감소시킵니다.
일반적으로 SGD가 ALS보다 쉽고 빠르지만, 다음의 두 가지 경우에는 ALS가 더 유리합니다.
- 병렬 처리(Parallelization)를 사용할 수 있는 경우: ALS에서 시스템은 각 를 다른 아이템 요인들과 독립적으로 계산하며, 각 역시 독립적으로 계산합니다. 이는 알고리즘의 대규모 병렬 처리를 가능하게 합니다.
- 암묵적 데이터(Implicit data) 중심의 시스템인 경우: 이 경우 훈련 세트를 희소(sparse)하다고 간주할 수 없으므로, 경사 하강법처럼 모든 훈련 사례를 하나씩 훑는 것은 실용적이지 않습니다. ALS는 이러한 경우를 효율적으로 처리할 수 있습니다.
편향 추가 (Adding Biases)
협업 필터링에서 행렬 분해 접근 방식이 갖는 이점 중 하나는 다양한 데이터의 측면과 애플리케이션 특유의 요구 사항을 처리하는 데 있어 유연하다는 점입니다. 이를 위해서는 동일한 학습 프레임워크를 유지하면서 식 (1)을 조정해야 합니다. 식 (1)은 서로 다른 평점 값을 생성하는 사용자와 아이템 간의 상호작용을 포착하려고 합니다. 그러나 관측된 평점 변동의 상당 부분은 상호작용과 무관하게 사용자 또는 아이템 자체와 관련된 효과로부터 발생하며, 이를 편향(biases) 또는 절편(intercepts)이라고 부릅니다.
예를 들어, 일반적인 협업 필터링 데이터에서는 어떤 사용자가 다른 사용자보다 더 높은 평점을 주는 경향이나, 어떤 아이템이 다른 아이템보다 더 높은 평점을 받는 체계적인 경향이 뚜렷하게 나타납니다. 결국 어떤 제품들은 다른 제품들보다 보편적으로 더 좋게(혹은 나쁘게) 인식되기 마련입니다.
따라서 전체 평점 값을 오직 형태의 상호작용으로만 설명하려는 것은 현명하지 못합니다. 대신 시스템은 개별 사용자나 아이템의 편향으로 설명할 수 있는 부분을 먼저 식별하고, 데이터의 진정한 상호작용 부분에 대해서만 요인 모델링(Factor modeling)을 적용합니다. 평점 rui에 포함된 편향의 1차 근사식은 다음과 같습니다.

평점 rui에 포함된 편향은 bui로 표기하며 사용자 및 아이템 효과를 설명합니다. 전체 평균 평점은 로 표기하며, 매개변수 와 는 각각 평균으로부터 관측된 사용자 와 아이템 의 편차를 나타냅니다.
예를 들어, 영화 <타이타닉>에 대한 사용자 '조(Joe)'의 평점을 예측한다고 가정해 봅시다. 모든 영화의 전체 평균 평점 가 3.7점이라고 합시다. 또한 <타이타닉>은 평균적인 영화보다 우수하여 평균보다 0.5점 높게 평가받는 경향이 있습니다. 반면, 조는 비판적인 사용자여서 평균보다 0.3점 낮게 점수를 주는 경향이 있습니다. 이 경우 조가 매길 <타이타닉>의 평점 예측값은 3.9점()이 됩니다.
편향을 추가하여 식 (1)을 확장하면 다음과 같습니다.

여기서 관측된 평점은 전체 평균, 아이템 편향, 사용자 편향, 사용자-아이템 상호작용이라는 네 가지 구성 요소로 분해됩니다. 이를 통해 각 구성 요소는 자신과 관련된 신호만을 설명할 수 있게 됩니다. 시스템은 다음의 제곱 오차 함수를 최소화함으로써 학습합니다.
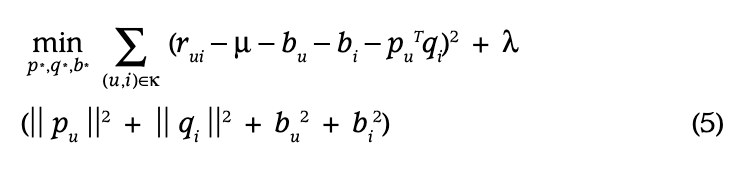
추가적인 정보 (Additional Input Sources)
시스템은 종종 많은 사용자가 매우 적은 수의 평점만을 제공하여 그들의 취향에 대한 일반적인 결론을 내리기 어려운 콜드 스타트 문제에 직면하게 됩니다. 이 문제를 완화하는 한 가지 방법은 사용자에 대한 추가적인 정보원을 통합하는 것입니다. 추천 시스템은 사용자의 선호도에 대한 통찰을 얻기 위해 암묵적 피드백을 사용할 수 있습니다. 실제로 시스템은 사용자의 명시적인 평점 제공 의사와 상관없이 행동 정보를 수집할 수 있습니다.
유통업체는 고객이 제공하는 평점 외에도 구매 이력이나 브라우징 기록을 사용하여 그들의 성향을 파악할 수 있습니다.
단순화를 위해 불리언(Boolean) 형태의 암묵적 피드백 사례를 가정해 봅시다. N(u)는 사용자 가 암묵적인 선호도를 표현한 아이템들의 집합을 나타냅니다. 이러한 방식으로 시스템은 사용자가 암묵적으로 선호했던 아이템들을 통해 사용자 프로필을 작성합니다. 이때 새로운 아이템 요인 집합이 필요한데, 각 아이템 는 벡터 와 연관됩니다. 따라서 N(u)에 속한 아이템들에 선호도를 보인 사용자는 다음의 벡터로 특징지어집니다
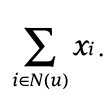
이 합계를 정규화하는 것이 유용한 경우가 많으며, 예를 들어 를 사용합니다.
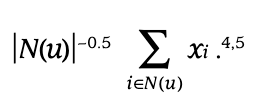
또 다른 정보원은 인구통계학적 정보와 같이 알려진 사용자 속성(attributes)입니다. 다시 단순하게 사용자 가 성별, 연령대, 우편번호, 소득 수준 등을 나타내는 속성 집합 A(u)에 대응되는 불리언 속성을 고려해 봅시다. 각 속성에는 고유한 요인 벡터 가 대응되며, 사용자와 연관된 속성 집합을 통해 사용자를 다음과 같이 묘사합니다:

행렬 분해 모델은 보강된 사용자 표현(enhanced user representation)을 통해 모든 신호원을 통합해야 합니다:
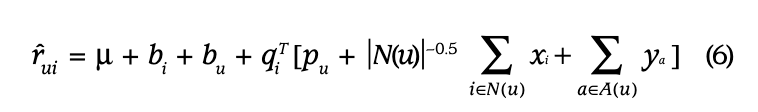
앞선 예시들은 데이터 부족이 더 흔하게 발생하는 사용자 표현을 강화하는 것에 초점을 맞췄지만, 필요한 경우 아이템에 대해서도 유사한 처리를 할 수 있습니다.
시간적 역동성 (Temporal Dynamics)
지금까지 제시된 모델들은 정적(static)이었습니다. 하지만 현실에서 제품에 대한 인식과 인기도는 새로운 선택지가 등장함에 따라 끊임없이 변화합니다. 마찬가지로, 고객의 성향도 진화하며 그로 인해 자신의 취향을 재정의하게 됩니다. 따라서 시스템은 사용자-아이템 상호작용의 역동적이고 시간에 따라 변하는 특성을 반영하는 시간적 효과(temporal effects)를 고려해야 합니다.
행렬 분해 접근 방식은 시간적 효과를 모델링하는 데 매우 적합하며, 이를 통해 정확도를 크게 향상시킬 수 있습니다. 평점을 별개의 항들로 분해함으로써 시스템은 다양한 시간적 측면을 개별적으로 처리할 수 있게 됩니다. 구체적으로 아이템 편향 , 사용자 편향 , 그리고 사용자 선호도 p*u(t)가 시간에 따라 변하는 항들입니다.
첫 번째 시간적 효과는 아이템의 인기도가 시간이 지남에 따라 변할 수 있다는 사실을 다룹니다. 예를 들어, 특정 배우가 새로운 영화에 출연하는 것과 같은 외부 사건에 의해 영화의 인기도가 오르내릴 수 있습니다. 따라서 이 모델들은 아이템 편향 를 시간의 함수로 취급합니다.
두 번째 효과는 사용자가 시간이 흐름에 따라 자신의 기준 평점을 바꾸는 것을 허용합니다. 예를 들어, 예전에는 평균적인 영화에 '4점'을 주던 사용자가 이제는 동일한 수준의 영화에 '3점'을 줄 수 있습니다. 이는 사용자의 평점 척도가 자연스럽게 변했거나, 최근에 본 다른 영화들과 비교하여 평점을 매기는 경향, 혹은 한 가구 내에서 평점을 매기는 실제 주체(가족 구성원)가 바뀌는 상황 등을 반영할 수 있습니다. 따라서 이 모델들에서 매개변수 는 시간의 함수가 됩니다.
시간적 역동성은 여기서 그치지 않고 사용자의 선호도, 즉 사용자와 아이템 간의 상호작용에도 영향을 미칩니다. 사용자는 시간이 지나면서 선호도를 바꿉니다. 예를 들어, 심리 스릴러 장르의 팬이었던 사람이 1년 후에는 범죄 드라마의 팬이 될 수 있습니다. 마찬가지로 인간은 특정 배우나 감독에 대한 인식을 바꿉니다. 모델은 사용자 요인(벡터 )을 시간의 함수로 설정하여 이 효과를 반영합니다. 반면, 아이템은 인간과 달리 본질적으로 정적이기 때문에 아이템의 특성 는 정적인 상태로 유지합니다.
시간에 따라 변하는 매개변수들을 정확하게 수식화하면, 식 (4)는 시간 에서의 평점을 예측하는 동적 규칙으로 대체됩니다.
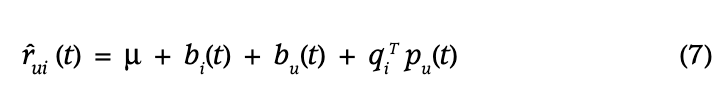
'ML > 데이터 분석' 카테고리의 다른 글
| [airflow] certified (0) | 2025.10.29 |
|---|---|
| [airflow] Branching (0) | 2025.10.27 |
| CoxPHFitter (2) | 2025.07.23 |
| 2. 3점 슛이 코트를 지배하는가? (1) | 2025.07.05 |
| 1. 영화관은 정말 망해가고 있는걸까? (0) | 2025.06.29 |


