서문
https://leetcode.com/problems/implement-strstr/ 의 문제를 풀면서 의문이 들었다. 해당 문제는 이중 for문을 사용하면 timeout이 발생한다.
python로 문제를 푼다면 find 함수를 사용하여 간단히 풀 수 있다. 각 언어별로 find(text, pattern)는 (문자열 text에 특정 문자열 pattern의 위치를 리턴하는 함수)가 있을텐데 pytho은 "어떤 알고리즘을 사용하길래 문자열을 빠르게 찾는걸까?"에서 시작했다.
언어별 결과를 빠르게 알고 싶다면 글의 마지막 번외를 보시면 됩니다.
문자열 검색 알고리즘에 어떤것들이 있는지, 차근차근 공부를 해보는 문서이다.
1. Brute force search
무차별 문자열 검색은 매우 기본적인 하위 문자열 검색 알고리즘 입니다. 무차별 문자열 검색의 좋은점은 텍스트 또는 패턴의 사전 처리가 필요하지 않습니다.
무차별 대입검색은 하위 문자열 일치에서 패턴의 첫 번째 문자가 있는 텍스트의 모든 단일 문자를 확인합니다. 두 문자열 사이에 일치가 있으면 아래 그림과 같이 패턴의 두 번째 문자와 텍스트의 다음 문자 사이의 비교를 이동합니다.
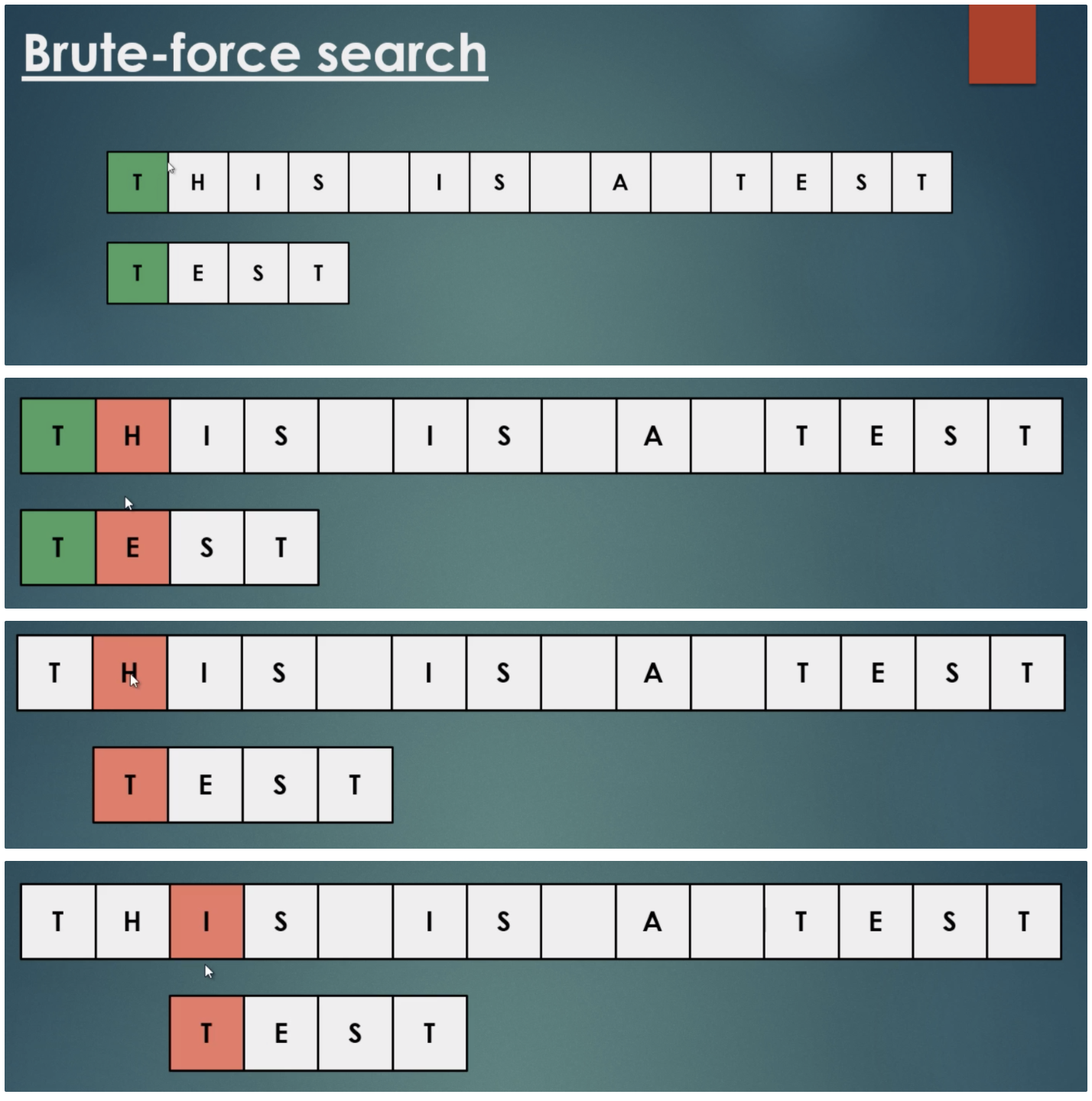
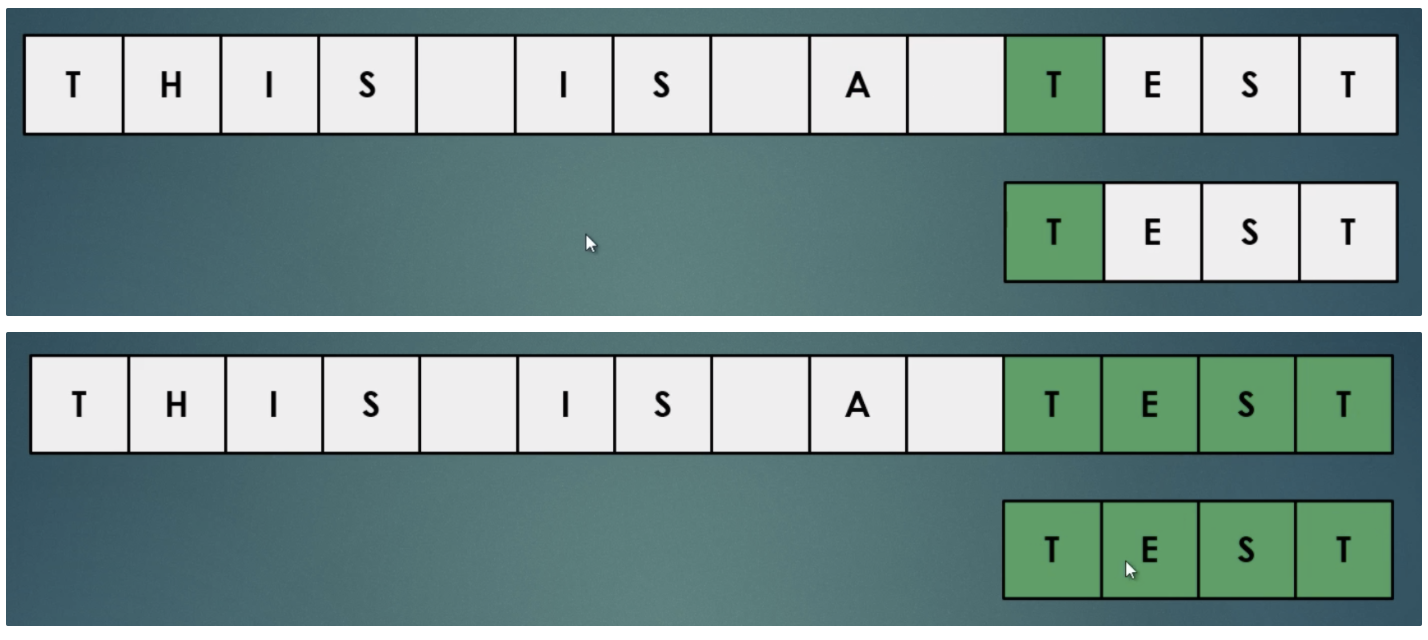
문제는 매우 느리다는 것입니다. 먼저 텍스트에서 모든 문자를 확인해야 합니다. 반면에 텍스트 문자와 패턴의 첫 번째 문자가 일치하는 것을 발견하더라도 패턴의 문자별로 계속 확인하여 텍스트에 있는지 찾습니다.

이러한 문제를 피하기 위해 해시를 사용합니다. 모든 패턴과 텍스트의 문자별 비교를 피하고 한번에 비교 하기 위해 해시 함수를 사용합니다.
또 다른 문제는 긴 문자열의 경우 짧은 해시를 기대할 수 없다는 것입니다.
2. Rabin-karp(라빈 카프) 알고리즘
Rabin–Karp algorithm 은 해싱(Hashing)을 사용해서 문자열에서 특정 패턴과 일치하는지 찾아주는 알고리즘입니다.

기본적인 알고리즘은
- 비교할 문자열과 패턴을 Hash function을 통해 해시값으로 변환
- 해시값의 비교를 통해서 문자열이 일치하는지 확인
- 일치하지 않으면 다음 문자열로 넘어가고
- 일치한다면 해당 문자열과 패턴의 1:1 매칭을 통해서 최종적으로 일치하는지 확인
- 해시값이 같지만 다른 문자열인 경우를 대비해서 해시값이 일치하는 경우에는 일대일 매칭으로 일치하는지 확인
라빈카프에서는 패턴과 일치하지 않는 부분을 빠르게 걸러주기 위해서 rolling hash를 hash function으로 사용합니다.
def RabinKarp(s, pattern):
pattern_hash = hash(pattern) # 1. 패턴의 hash값을 구한다
n = len(pattern)
for i in range(len(s)):
s_hash = hash(s[i:i+n]) # 2. 문자열의 패턴의 길이만큼 hash값을 구한다.
if pattern_hash == s_hash: # 2-2 : 해쉬값이 일치하다면
if pattern == s[i:i+n]: # 2-2-1 : 패턴과 문자열이 일치한지 확인
return i
return -1복잡도
n 은 텍스트 길이, m 은 패턴의 길이일때, Rabin-Karp 알고리즘은 O(nm)의 복잡도를 가지고 있습니다.
장점
- 무차별 대입 매칭보다 빠르지 않지만 실제로는 복잡도가 O(n+m)
- 좋은 해싱 기능을 사용하면 매우 효과적일 수 있으며 구현하기 쉬움
단점
- O(n+m)보다 빠른 문자열 일치 알고리즘이 많음
- 사실상 무차별 대입 일치만큼 느리고 추가 공간이 필요함
3. KMP (Knuth-Morris-Pratt)
KMP알고리즘은 "불일치가 발생하기 직전까지 같았던 부분은 다시 비교하지 않고 건너뛴 후 패턴 매칭(검색)을 진행하자!" 는 것입니다. 비교 횟수를 줄이고, 검색 알고리즘의 효율성을 높이자는 것이 이 알고리즘의 의도입니다.

문자열 ABACABAACABACABAC 에서 패턴 ABACABAC를 찾는다고 가정하겠습니다.

7글자가 일치하다가 마지막 글자가 다릅니다. 그럼 이번에는 8칸을 건너뛰느냐? 찾으려는 패턴과 동일하게 시작하는 문자가 5번에 위치(ABA~~)하고 있으므로, 8칸을 뛰어넘으면 탐색이 누락되게 됩니다.
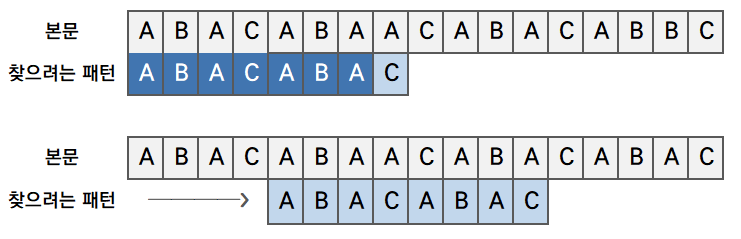
따라서, KMP에서는 8칸이 아닌 4칸을 건너뛰고 다시 매치을 시작합니다.
이렇게 몇칸을 건너뛰는지 판단하기 위해 실패 함수를 사용합니다.
Partial match table(failure function)
실패함수는 찾으려는 패턴의 i번째 글자까지 중에서 일치하는 접두사(prefix)와 접미사(suffix) 중에서 최대의 길이를 값으로 가집니다.
그래서 방금 예제에서 문자열 "ABACABAC"의 실패함수는 다음과 같습니다.
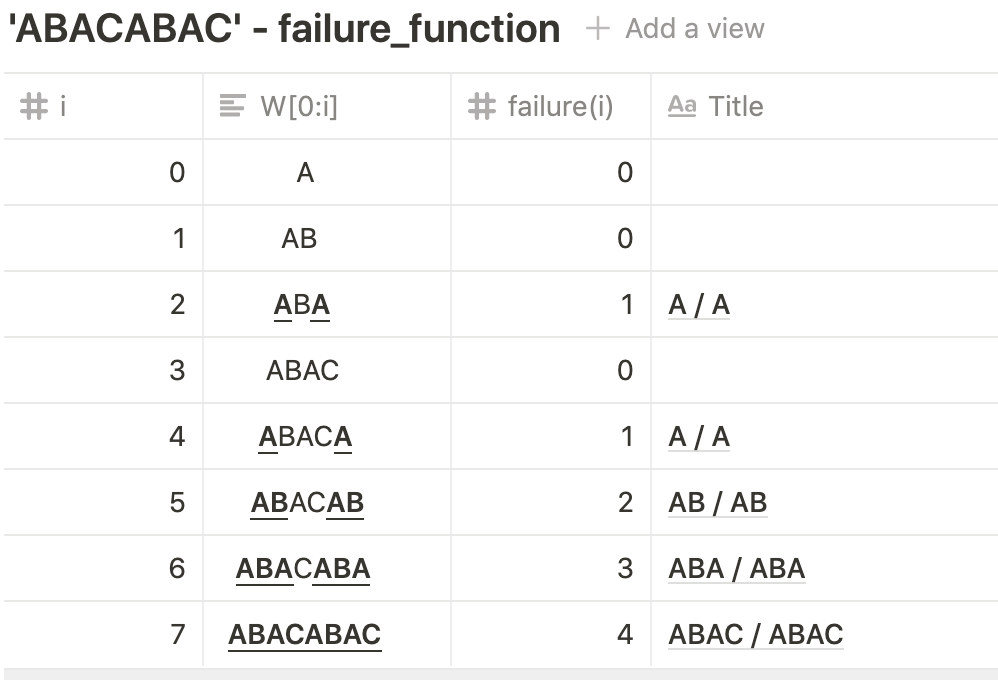
다른예제 패턴 "issip"의 failure_function 는 다음과 같다.

다시 위의 그림에서 i == 7일때 실패가 일어났으므로 실패함수에서 그 이전단계인 i가 6일때의 값인 3, 그리고 다음칸인 +1 칸하여 4번째 칸으로 이동합니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
from collections import defaultdict
def failure_function(pattern):
m = len(pattern)
d = defaultdict(int)
begin = 1
matched = 0
while begin + matched < m:
if pattern[begin + matched] == pattern[matched]:
matched += 1
d[begin + matched - 1] = matched
else:
if matched == 0:
begin += 1
else:
begin += matched - d[matched - 1]
matched = d[matched - 1]
return d
def KMP(word, pattern):
table = failure_function(pattern)
results = []
p = 0
for idx in range(len(word)):
while p > 0 and word[idx] != pattern[p]:
p = table[p - 1]
if word[idx] == pattern[p]:
if p == len(pattern) - 1:
results.append(idx - len(pattern) + 2)
p = table[p]
else:
p += 1
return results
|
cs |
복잡도
KMP 알고리즘에서 접두, 접미사의 길이를 이용하여 탐색을 건너뛰는 아이디어이므로 문자열의 길이에 비례하게 됩니다.
원본 문자열의 길이가 N, 탐색 문자열의 길이가 M 이라면 최종적인 시간 복잡도는 O(N + M) 이 됩니다.
장점
- 무차별 대입 매칭보다 빠르지 않지만 실제로는 복잡도가 O(n+m)
- 구현하기 쉬움
단점
- failure_function 별도의 메모리 필요
4. Boyer-Moore
Boyer–Moore 알고리즘은 KMP알고리즘과 달리 오른쪽에서 왼쪽으로 비교 검사하며, 효과적으로 패턴문자열을 이동할수 있는 방법을 제시 합니다.
이 알고리즘은 크게 두 가지 이동방법이 있습니다.
- Bad Character Shift (나쁜 문자 이동)
- Good Suffix Shift (착한 접미부 이동)
- BC(Bad Character) & GS(Good Suffix) 혼합 사용
여기에서는 첫번째 나쁜 문자이동을 소개해드리겠습니다. 두번째 접미부 이동의 설명은 링크를 확인하세요.
나쁜 문자 이동
나쁜 문자이동에는 두가지 패턴을 적용합니다.
- Bad Character가 패턴의 문장열에 존재할 때
- Bad Character가 패턴의 문자열에 존재하지 않을 때
여기에서 Bad Character는 패턴의 현재 문자와 일치하지 않는 텍스트의 문자를 가르킵니다.

먼저 1번 Bad Character가 패턴의 문자열에 존재할 때입니다.
- 문자열과 패턴을 오른쪽에서 왼쪽으로 문자 일치를 확인합니다.
- 문자열과 패턴의 문자가 다른 위치는 b로 문자열 → "C" / 패턴 → "T"를 나타내고 있습니다.
- Bad Character는 "C"가 됩니다.
- 패턴의 문자열 중 Bad Character가 있는지 확인합니다. 여러개일 경우 가장 오른쪽에 있는것을 선택합니다.
- 2번째에 "C"가 존재합니다. 문자열 "C"의 위치로 패턴의 "C"를 일치시킵니다.

위의 스탭에서 "C"를 같은 위치로 일치 시켰습니다.
이번엔 2번 Bad Character가 패턴의 문자열에 존재하지 않을 때 입니다.
- 문자열과 패턴을 오른쪽에서 왼쪽으로 문자 일치를 확인합니다.
- 문자열과 패턴의 문자가 다른 위치는 b로 문자열 → "A" / 패턴 → "G"를 나타내고 있습니다.
- Bad Character는 "A"가 됩니다.
- 패턴의 문자열 중 Bad Character가 있는지 확인합니다. 없다면 패턴의 문자열을 현재 "A"보다 뒤로 이동 시킵니다.

직접 해보시면 이해가 됩니다!! → https://personal.utdallas.edu/~besp/demo/John2010/boyer-moore.htm
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
def skip_table(text, pattern):
d = defaultdict(int)
for letter in set(text):
d[letter] = pattern.rfind(letter)
return d
def boyer_moore(text, pattern):
d = skip_table(text, pattern)
m = len(pattern)
n = len(text)
i = m - 1
j = m - 1
result = []
while i < n:
if text[i] == pattern[j]:
if j == 0:
result.append(i+1)
i -= 1
j -= 1
else:
i = i + m - min(j, d[text[i]]+1)
j = m - 1
return -1
|
cs |
복잡도
이 알고리즘은 항상 2)의 경우가 나오는 최적의 경우, 항상 패턴을 m만큼 이동시키므로,
시간복잡도는 최적의 경우 O(n/m) / 최악의 경우 O(nm) 입니다
(n: 텍스트의 길이, m: 패턴의 길이)
장점
- 최고의 성능을 발휘 가능 O(n/m)
단점
- 최악의 경우 KMP보다 느려질수 있음
끝!
| 번외
- 이 외에도 문자열 검색 알고리즘엔 Trie, 이진탐색, Knuth-Morris-Pratt 등 다양한 알고리즘이 있지만 결국 boyer-moore가 짱짱맨이다.
- 혹시나 코딩 테스트때 특정 문자를 찾아야 한다면 언어의 find()를 믿고 쓰자. 진짜 빠르고, 메모리도 효율적이다.
1. Mysql의 LIKE는 Turbo Boyer-Moore를 사용한다. → 공식문서
If you use … LIKE ‘%string%’ and string is longer than three characters, MySQL uses the Turbo Boyer-Moore algorithm to initialize the pattern for the string and then uses this pattern to perform the search more quickly.
2. postgresql의 LIKE도 Boyer-Moore-Horspool 를 사용한다. → 문서
3. Cpython의 find도 Boyer-Moore 로 구현되어 있다. → 소스
4. java - StringUtils.contains() / golang - find()도 Boyer-Moore 로 구현되어 있다
결국 Boyer-moore로 천하 통일!!
진짜 끝!
참조 사항
https://hooongs.tistory.com/304
https://bblackscene21.tistory.com/3?category=911534
https://bblackscene21.tistory.com/4?category=911534
https://linuxgazette.net/164/sephton.html
https://www.postgresql.org/docs/9.5/geqo-pg-intro.html
https://junstar92.tistory.com/202?category=884881
https://1ambda.github.io/algorithm/algorithm-part2-4/
'뇌세포덩어리"" > 알고리즘' 카테고리의 다른 글
| [leetcode] dfs / bfs 재밌는 문제들 (0) | 2023.02.03 |
|---|---|
| [leetcode] dfs/bfs 섬 문제들 (0) | 2023.02.01 |
| 탐색 (선형 / 이진 / 이진트리) (0) | 2016.05.18 |
| 정렬 알고리즘 ( 버블 / 선택 / 삽입 / 퀵) (0) | 2016.05.16 |
| 중복되는 가장 긴~ 문자열 찾기 알고리즘(2) (5) | 2013.12.08 |