부동 소수점 오류 예
0.1 == 0.1 # True
0.2 == 0.1+0.1 # True
0.3 == 0.1+0.1+0.1 # False
0.4 == 0.2+0.2 # True
0.5 == 0.2+0.2+0.1 # True
0.6 == 0.2+0.2+0.2 # False
0.9 == 0.5+0.4 # True
0.9 == 0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1 # False
0.1을 100번 더하면 10이 나와야 되는데... 0.1을 정확히 표현할 수 없기 때문에 발생하는 오류입니다.
result = 0.0
for i in range(0, 100):
result += 0.1
print(result)

이 모든것은 부동 소수점에서 발생하는 문제이다.
소수점 연산은 정확한 연산을 할 수 없어 근삿값으로 대체되기 때문이다.
파이썬에서는 아래와 같이 해결한다.
1. epsilon 이용
부동소수점으로 실수를 표현하면 소숫점 이하가 무한히 반복되기 때문에,
특정 시점에 반올림하여 실제 값과 비슷한 근삿값을 구하게 된다.
이렇게 실제 값과 근사값 사이에 발생하는 오차를 반올림 오차(rounding error)라고 하는데,
이 차이는 항상 머신 엡실론(machine epsilon) 값 보다 작다.
이와 같은 특성을 이용해서 실수비교를 수행하면 된다.
근사 값에서 실제 값을 뺀 값이 머신 엡실론보다 작다면, 이는 같은 값으로 취급하면 된다.
머신 엡실론 값은 sys.float_info.epsilon에 저장되어있다.
|
1
2
3
4
5
6
7
8
9
10
|
import sys
def compare_floating_point(approx, actual):
return (True if abs(approx - actual) <= sys.float_info.epsilon else False)
print(f"0.1 + 0.2 : {0.1 + 0.2}")
print(f"0.1 + 0.2 == 0.3 : {compare_floating_point(0.1 + 0.2, 0.3)}")
0.1 + 0.2 : 0.30000000000000004
0.1 + 0.2 == 0.3 : True
|
cs |
2. math.isclose
두 실수가 같은지 판단할 때 사용한다.
|
1
2
3
|
import math
math.isclose(0.1 + 0.2, 0.3) # True
|
cs |
3. Decimal으로 정확한 자릿수 표현하기
반올림 오차가 없는 고정소수점을 사용하려면 decimal 모듈의 Decimal을 사용하면 된다. Decimal은 숫자를 10진수로 처리하여 정확한 소수점 자릿수를 표현합니다.
|
1
2
|
from decimal import Decimal
Decimal('0.1') + Decimal('0.2') == Decimal('0.3')
|
cs |
4. Fraction로 유리수 표현하기
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
>>> from decimal import Decimal
>>> from fractions import Fraction
>>> Fraction.from_float(0.1)
Fraction(3602879701896397, 36028797018963968)
>>> (0.1).as_integer_ratio()
(3602879701896397, 36028797018963968)
>>> Decimal.from_float(0.1)
Decimal('0.1000000000000000055511151231257827021181583404541015625')
>>> format(Decimal.from_float(0.1), '.17')
'0.10000000000000001'
|
cs |
번외
Fraction으로 분수 표현하기
순환소수는 고정소수점이라도 정확히 표현할 수 없다. 이때는 fractions 모듈의 Fraction을 사용하여 분수로 표현하면 된다.
|
1
2
3
4
5
6
|
>>> from fractions import Fraction
>>> Fraction('10/3') # 10을 3으로 나누면 순환소수 3.33333...이지만 분수 3분의 10으로 표현 Fraction(10, 3)
10/3
>>> print(type(Fraction('10/3')))
<class 'fractions.Fraction'>
|
cs |
부동소수점에서의 반올림 ( IEEE 754-1985에서의 반올림 정의)
|
1
2
3
4
5
|
>>> round(0.5) # 0
>>> round(1.5) # 2
>>> round(2.5) # 2
>>> round(3.5) # 4
>>> round(4.5) # 4
|
cs |
우리가 흔히 아는 반올림 함수인 round()의 결괏값들이다. 파이썬 버전마다 결과가 다르지만, 3.x버전에서의 결괏값은 위와 같다.
먼저 부동소수점에서의 반올림은 IEEE-754에서 정의되어 있다. IEEE 754에 정의된 반올림은 아래 5가지이다.
1. round up
round up은 반올림 처리시 +∞ 방향으로 올림 처리를 한다.
그렇기 때문에 음수인 경우에는 0의 방향으로 향하기 때문에 절댓값을 기준으로 본다면 숫자가 버림 처리가 된다

2. round down
round down은 반올림 처리시 -∞ 방향으로 내림 처리를 한다.
그렇기 때문에 음수인 경우에는 절대값 기준으로 본다면 숫자가 올림 처리가 된다.

3. round toward zero
round toward zero는 반올림 처리시 항상 0의 방향으로 가장 가까운 숫자를 선택한다.
절댓값을 기준으로 본다면 원래의 값보다 절댓값이 작거나 같은 값 중에 가장 큰 숫자를 선택하게 된다. 즉 항상 버림 처리가 된다.

4-1. round to nearest, ties to even (파이썬이 택한 반올림)
round to nearest는 말 그대로 가장 가까운 값으로 반올림을 하는 것인데 IEEE 754에서는 가장 가까운 값의 기준으로 두 가지로 분류했다.
하나는 ties to even으로 가장 가까운 값이 2개인 경우( 예를 들어 0.5인 경우 가장 가까운 값은 0과 1) 가수부의 마지막 자리가 짝수인 값을 선택하는 것이다.
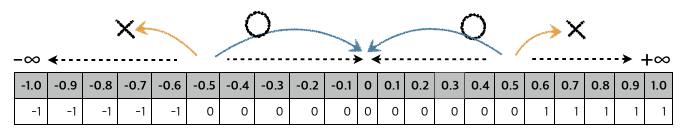
4-2. round to nearest, ties away from zero
가장 가까운 값이 2개인 경우 절대값 기준으로 가장 큰 값을 선택한다.

파이썬에서 정의한 반올림이 사실 우리가 아는 반올림과 다르다.
파이썬은 ties to even 로 우리가 초등학교 때 배운 ties away from zero과 상당한 차이가 있다. 즉 큰 수가 짝수일 경우에만 높게 선택되는 것이다.
이를 회피하기 위해서는 딱히 기본 내장 함수에서 지원하진 않으며, 해당 소수점에서 0.5일 경우 round(0.5+0.01)으로 변경하여 반올림하면 우리의 예상대로 동작하는 페이크 형식으로 작성해야 한다.
이를 분명히 알고 코딩해야 나중에 잠을 더 잘수 있다.
참고
'app > python' 카테고리의 다른 글
| pickle (0) | 2021.06.28 |
|---|---|
| pip multiple versions of dependency resolver problem (1) | 2021.06.10 |
| array의 연산을 빠르게 하는 방법 (0) | 2021.04.09 |
| Peephole optimization (0) | 2020.04.09 |
| The internals of Python string interning (0) | 2020.04.01 |


